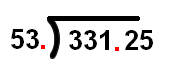Everyday math Long division

This section is a brief overview of math division. It covers the concept of sharing in equal amounts, the basic division operation and long division. The sections most relevant to you will depend on your child’s level. Use the information and resources to help review and practice what your child’s teacher will have covered in the classroom.

Introducing division

When you start teaching division to your child you should introduce division as being a sharing operation where objects are shared (or divided) into a number of groups of equal number. Below is a video that shows examples of the types of exercise you can try with your child as you introduce division to them.

Once you have build an understanding of the concept of division you can try using these division worksheets.When teaching early division you should also discuss that division has an opposite. Discuss how division is about separating sets, while the opposite type of math, called multiplication is about combining sets. Explore this relationship with your child as it will be important when recalling basic facts to solve division problems. Introduce fact families (e.g. 5 x 3 =15, 3 x 5 = 15, 15 ÷ 3 = 5, 15 ÷ 5 = 3).

Dividing numbers

After your child grasps the concept of dividing and the relationship with multiplication you can start working with numbers. Be sure your child is familiar with the format and signs for division

With the concept grasped, teaching division will become more about guided practice to help your child to become familiar with the division operation (although it’s really going to be a different type of multiplication practice.) Start by practicing division by 1, 2 and 3 and then gradually move up to 9. Use the worksheets to help.

Division with remainders

Your child will most likely come across or ask about situations where division “doesn’t work.” These can be explained with the introduction of the remainder. It is an important idea to understand as the division of larger numbers will require the “carrying” of this remainder.

Teaching division with larger numbers

There are a number of methods for dividing larger numbers. One of these is shown below:

These printable worksheets will provide practice with similar types of division problems.

Long Division

There are different methods for dividing multi-digit numbers (long division). One way is a combination of estimation/ trial and error and multiplication. Another method is well explained and illustrated on mathisfun.com.

There, we studied problems on long division by a single digit number. Here, we extend that study by solving Long Division of a Five digit number by a single digit number. We also introduce long division by two digit numbers.

Example 1

Divide 79865 by 8.

Solution:

Step 1:

Here first digit of dividend is 7 which is less than the divisor 8. So we see the first two digits of the dividend which is 79. We find how many times 8 divides 79. We know 9 x 8 = 72. We put 9 in the right bracket and 72 below 79 of  the dividend. 72 subtracted from 79 gives 7.

Dividend
 Divisor   8 )   79865   ( 9   
                 72
                 -----
                  7

Step2: Learning Long Division

We descend the next digit of the dividend, 8 to the right of 7 to make it 78. We know 8 divides 78,
nine times. 9 x 8 = 72. We write 9 in the right bracket after 9 and 72 below 78.

72 subtracted from 78 gives 6.

Dividend
 Divisor   8 )   79865   ( 99   
                 72
                 -----
                  78
                  72    
                 -----  
                   6 

Step 3: Learning Long Division

We descend the next digit of the dividend, 6 to the right of 6 to make it 66. We know 8 divides 66,
eight times. 8 x 8 = 64. (Note that 9 x 8 = 72 exceeds 66.)
We write 8 in the right bracket after 99 and 64 below 66. 64 subtracted from 66 gives 2.

Dividend
 Divisor   8 )   79865   ( 998
                 72
                 -----
                  78
                  72    
                 -----  
                   66 
                   64   
                 ----- 
                    2

Step 4: Learning Long Division

We descend the next (last) digit of the dividend, 5 to the right of 2 to make it 25. We know 8 divides 25, three times. 3 x 8 = 24. (Note that 4 x 8 = 32 exceeds 25.)
We write 3 in the right bracket after 998 and 24 below 25. 24 subtracted from 25 gives 1 which is the remainder.

Dividend
 Divisor   8 )   79865   ( 9983   Quotient    
                 72
                 -----
                  78
                  72    
                 -----  
                   66 
                   64   
                 ----- 
                    25
                    24
                 ----- 
                      1   Remainder
                 ----- 

Thus 79865 ÷ 8 gives quotient  = 9983 and remainder = 1. Ans.

Check:
Verify whether
Dividend = Divisor x Quotient + Remainder
is satisfied or not.

R.H.S. = Divisor x Quotient + Remainder
= 8 x 9983 + 1 = 9983 x 8 + 1

To Find 9983 x 8 :

9983
         8                                  
     ------           2 6 7
     79864
     ------

R.H.S. = Divisor x Quotient + Remainder = 8 x 9983 + 1 = 79864 + 1 = 79865 = Dividend = L.H.S. (Verified. )

Example 2 of Learning Long Division

Divide 983 by 29.

Solution:

Step 1: Learning Long Division

Here the divisor is a two digit number, 29. So we see the first two digits of the dividend which is 98. We have to find how many times 29 divides 98. Unlike in the previous sums where the knowlegde of Multiplication Tables was sufficient to decide how many times the divisor divides the number, here we have to calculate to decide.

We don't remember (not supposed to remember) 29 table.29 is near 30. We know 3 x 30 = 90 which is near 98. (To find 3 x 30, we simply find 3 x 3 and then put a 0 to the right of  the result.) So we try 3 x 29. 

Here, we use the knowledge of Multiplication.

29
       3                             
     ---           2
     87
     ---

87 is less than 98 by 11 only. So 4 times 29 is not required. We have 3 x 29 = 87. We put 3 in the right bracket and 87 below 98 of the dividend.
87 subtracted from 98 gives 11.

Dividend
 Divisor   29 )   983   ( 3
                  87
                 -----
                  11

Step 2: Learning Long Division
We descend the next (last) digit of the dividend, 3 to the right of 11 to make it 113. We know 3 x 29 = 87.
Let us find 4 x 29:

29
       4                             
     ---           3
     116
     ---

4 x 29 = 116 exceeds 113. So 29 divides 113, three times and 3 x 29 = 87. We write 3 in the right bracket
after 3 and 87 below 113. 87 subtracted from 113 gives 26 which is the remainder.

Dividend
 Divisor   29 )   983   ( 33   Quotient    
                  87
                 -----
                  113
                   87    
                 -----  
                   26   Remainder 
                 -----   

Thus 983 ÷ 29 gives quotient = 33 and remainder = 26. Ans.

Check:
Verify whether
Dividend = Divisor x Quotient + Remainder
is satisfied or not.

R.H.S. = Divisor x Quotient + Remainder
= 29 x 33 + 26

To Find 29 x 33 :

29
      33                            
     ----           2
      87
     87
     ----
     957
     ----

R.H.S. = Divisor x Quotient + Remainder = 29 x 33 + 26 = 957 + 26 = 983 = Dividend = L.H.S. (Verified.) 

Example 3

Divide 5892 by 37.

Solution:

Step 1:

Here the divisor is a two digit number, 37. So we see the first two digits of the dividend which is 58. We have to find how many times 37 divides 58. 1 x 37 = 37; 2 x 37 is more than 2 x 30 i.e. 60 > 58.
So 37 divided 58 one time.We have 1 x 37 = 37. We put 1 in the right bracket and 37 below 58 of the dividend.

37 subtracted from 58 gives 21.

Dividend
 Divisor   37 )   5892   ( 1
                  37
                 -----
                  21

Step 2:
We descend the next digit of the dividend, 9 to the right of 21 to make it 219. 37 is near 40 and we know 5 x 40 = 200 which is near 219.
Let us find 5 x 37 and 6 x 37.

37
       5                             
     ---           3
     185
     ---

37
       6                             
     ---           4
     222
     ---

6 x 37 = 222 exceeds 219. So 37 divides 219, five times and 5 x 37 = 185. We write 5 in the right bracket
after 1 and 185 below 219.
185 subtracted from 219 gives 34.

Dividend
 Divisor   37 )   5892   ( 15
                  37
                 -----
                  219
                  185
                 -----
                   34

Step 3 : Teaching Long Division
We descend the next (last) digit of the dividend, 2 to the right of 34 to make it 342. 37 is near 40 and we know 8 x 40 = 320 which is near 342.
Let us find 8 x 37 and 9 x 37.

37
       8                             
     ---           5
     296
     ---

37
       9                             
     ---           6
     333
     ---

9 x 37 = 333 is less than 342. So 37 divides 342, nine times and 9 x 37 = 333. We write 9 in the right bracket after 15 and 333 below 342. 333 subtracted from 342 gives 9 which is the remainder.

Dividend
 Divisor   37 )   5892   ( 159   Quotient
                  37
                 -----
                  219
                  185
                 -----
                   342
                   333
                  -----
                     9    Remainder
                  -----

Thus 5892 ÷ 37 gives quotient
= 159 and remainder = 9. Ans.

Check :
Verify whether
Dividend = Divisor x Quotient + Remainder
is satisfied or not.

R.H.S. = Divisor x Quotient + Remainder
= 37 x 159 + 9 = 159 x 37 + 9

To Find 159 x 37 :

159
       37                            
     ----           6    4
     1113      2    1
     477
     ----
     5883
     ----

R.H.S. = Divisor x Quotient + Remainder = 37 x 159 + 9 = 5883 + 9 = 5892 = Dividend = L.H.S. (Verified.)

As the number of digits of the dividend increases, the number of steps in the process increases. Except for that
the procedure is same.Teaching Long Division is done by the above three steps. Let us see another example in

which a six digit number is divided by a three digit number.

Example 4 of Teaching Long Division

Divide 609182 by 463.

Solution:

Step 1: Teaching Long Division

Here the divisor is a three digit number 463. So we see the first three digits of the dividend which is 609. We have to find how many times 463 divides 609. 1 x 463 = 463; 2 x 463 is more than 800 > 609. So 463 divides 609 one time.We have 1 x 463 = 463. We put 1 in the right bracket and 463 below 609 of the dividend. 463 subtracted from 609 gives 146. 

Dividend
 Divisor   463 )   609182   ( 1
                   463
                   ---
                   146

Step 2: Teaching Long Division
We descend the next digit of the dividend, 1 to the right of 146 to make it 1461. 463 is near 500 and we know 3 x 500 = 1500 which is near 1461.
Let us find 3 x 463.

463
        3                             
     ----           1
     1389
     ----

4 x 463 is more than 1600 which exceeds 1461. So 463 divides 1461, three times and 3 x 463 = 1389.
We write 3 in the right bracket after 1 and 1389 below 1461. 1389 subtracted from 1461 gives 72.

Dividend
 Divisor   463 )   609182   ( 13
                   463
                   ---
                   1461
                   1389
                   ----
                     72           
                       

Step 3: Teaching Long Division
We descend the next digit of the dividend, 8 to the right of 72 to make it 728. 1 x 463 = 463; 2 x 463 is more than 800 > 728. So 463 divides 728 one time.

We have 1 x 463 = 463.
We put 1 in the right bracket
after 13 and 463 below 728.
463 subtracted from 728 gives 265.

Dividend
 Divisor   463 )   609182   ( 131
                   463
                   ---
                   1461
                   1389
                   ----
                     728
                     463
                   -----
                     265

Step 4: Teaching Long Division
We descend the next (last) digit of the dividend, 2 to the right of 265 to make it 2652. 463 is near 500 and we know 5 x 500 = 2500 which is near 2652.
Let us find 5 x 463 and 6 x 463.

463
        5                             
     ----           1    3
     2315
     ----

463
        6                             
     ----           1    3
     2778
     ----

6 x 463 = 2778 exceeds 2652. So 463 divides 2652, five times and 5 x 463 = 2315. We write 5 in the right bracket after 131 and 2315 below 2652. 2315 subtracted from 2652 gives 337 which is the remainder.

Dividend
 Divisor   463 )   609182   ( 1315   Quotient
                   463
                   ---
                   1461
                   1389
                   ----
                     728
                     463
                   -----
                     2652
                     2315
                     -----  
                      337   Remainder
                     -----  

Thus 609182 ÷ 463 gives quotient
= 1315 and remainder = 337. Ans.

Check:
Verify whether
Dividend = Divisor x Quotient + Remainder is satisfied or not. R.H.S. = Divisor x Quotient + Remainder
= 463 x 1315 + 337 = 1315 x 463 + 337

To Find 1315 x 463 :

1315
         463                            
      ------           1    
        3945      3    1
       7890       2    1
      5260
      ------
      608845
      ------

R.H.S. = Divisor x Quotient + Remainder = 463 x 1315 + 337 = 608845 + 337 = 609182 = Dividend = L.H.S. (Verified.). Thus, with any Dividend and any Divisor, we can carry out the division by following the same procedure.

[Read More...]

Long division with decimals in divisor

Another type of division you’ll encounter is division with decimals in both the divisor and the dividend. It might look something like this:

In this situation, you move the decimal place the number of spaces in the divisor until the decimal is at the end of the number; you move the decimal the same number of spaces in the dividend: this does NOT necessarily mean the decimal will land at the end of the dividend. Here’s an example:

Your new problem looks like this (note the change in decimal places in both the divisor and dividend):

Now you continue to work the problem out, remembering to bring your decimal up into your quotient at the appropriate time (it will be in red in the diagram).

Thus, your final answer is simply 16.
Let’s try one more example of moving the decimal over in order to solve the problem.

becomes

After the decimals are moved, it looks like this:

After you move the decimals, continue the problem, like this:

Thus, your final answer is 6.25.

We’ve already practiced long division, but so far our answers have all come out even (in other words, our last subtraction problem ended in an answer of 0). However, sometimes our division problems will not come out evenly, and we will have another number (not 0) when we do the last subtraction problem. This leftover number is called a remainder, and it is written as part of the quotient. Follow along with this example:

The red circled number at the bottom our remainder. You do not have to circle the remainder; we just circled ours so that you know which number it is. After you have your remainder, you write it on top of the division bar, with an r in front of it, like this: 25 r 3.
When your division ends with a remainder, you must make sure that your remainder is less than your divisor. If your remainder is more than your divisor, you need to go back and check your division, because it is incorrect. We can still use our multiplication method to check our division; you will multiply the quotient (25) by the divisor (5), and then add our remainder to the answer to the multiplication problem, like this:

Let’s try that one more time. Here’s a new example:

Our answer to this problem is 23 r 1; note that we always write the remainder after the quotient, on top of the division bar. Also notice that our remainder (1) is smaller than our divisor (6).
Now let’s check our work, like this:

There are also several different ways to write remainders. The standard way is shown above, with an r in front of the number. However, you can also write remainders as fractions and as decimals.

Long Division with Remainders as Fractions

Now that you understand the basics of long division, you may be asked to write your remainder as a fraction. Don’t worry! It’s not hard at all. You’re going to do long division the same way—divide, multiply, subtract, bring down, and then you’re going to get a remainder. Instead of writing r and then the number, you are going to take your remainder and make it the numerator of a fraction. The denominator comes from the divisor—you use the same number you’re dividing by in your denominator.
Let’s look at the following example:

Notice that you do not use the r at all in front of your remainder when you’re turning it into a fraction. However, you do still write the fraction as part of the quotient (answer to your division problem).
Also, you would check this division problem the same way as a normal division problem; multiply the quotient (23) by the divisor (6) and then add the remainder (1). Do not do anything with the fraction in order to check this problem.

Long Division with Remainders as Decimals

Another way you may be asked to express a remainder is in the form of a decimal. When you’re asked to express your remainder as a decimal, you first complete division as usual, until you get to the point you usually end at, where you have nothing else to bring down. Instead of stopping here, however, you are going to keep going with division. You will add a decimal point (.) after the last number given in the dividend, and you will also place a decimal point in the quotient after the number you have so far. After the decimal in the dividend, you will add a zero (0) and continue division. You will keep adding zeroes until your subtraction step results in an answer of 0 as well. Follow along with this example:

Notice that we added a decimal after the 6 in the dividend, as well as a decimal after the 5 in our quotient. Then, we started adding zeroes to the dividend. This time, it only took us one added zero before our remainder was zero.
Now, let’s look at a problem where you’d have to add more than one zero to the dividend:

When you have your quotient with a decimal, you check the answer differently than if it had a remainder as a fraction or just a remainder written with r. Instead of adding the remainder separately, you just multiply the quotient (including decimal) by the divisor, like this:

[Read More...]

How to explain long division to children?

How to explain long division to children?

Solution for 531219 ÷ 579 - with remainder

Step 1 Long division works from left to right. Since 579 will not go into 5, a grey 0 has been placed over the 5 and we combine the first two digits to make 53. In this case, 53 is still too small. A further 0 is added above 3 and a third digit is added to make 531. Note the other digits in the original number have been turned grey to emphasise this. The closest we can get to 531 without exceeding it is 5211 which is 9 × 579. These values have been added to the division, highlighted in red.

0 0 0 9  rem 276 579 5 3 1 2 1 9 5 2 1 1

579 × table 1 × 579 = 579 2 × 579 = 1158 3 × 579 = 1737 4 × 579 = 2316 5 × 579 = 2895 6 × 579 = 3474 7 × 579 = 4053 8 × 579 = 4632 9 × 579 = 5211

Step 2 Next, work out the remainder by subtracting 5211 from 5312. This gives us 101. Bring down the 1 to make a new target of 1011.	9  rem 276 579 5 3 1 2 1 9 5 2 1 1 1 0 1 1
579 × table 1 × 579 = 579 2 × 579 = 1158 3 × 579 = 1737 4 × 579 = 2316 5 × 579 = 2895 6 × 579 = 3474 7 × 579 = 4053 8 × 579 = 4632 9 × 579 = 5211

Step 3 With a target of 1011, the closest we can get is 579 by multiplying 579 by 1. Write the 579 below the 1011 as shown.	9 1  rem 276 579 5 3 1 2 1 9 5 2 1 1 1 0 1 1 5 7 9
579 × table 1 × 579 = 579 2 × 579 = 1158 3 × 579 = 1737 4 × 579 = 2316 5 × 579 = 2895 6 × 579 = 3474 7 × 579 = 4053 8 × 579 = 4632 9 × 579 = 5211

Step 4 Next, work out the remainder by subtracting 579 from 1011. This gives us 432. Bring down the 9 to make a new target of 4329.	9 1  rem 276 579 5 3 1 2 1 9 5 2 1 1 1 0 1 1 5 7 9 4 3 2 9
579 × table 1 × 579 = 579 2 × 579 = 1158 3 × 579 = 1737 4 × 579 = 2316 5 × 579 = 2895 6 × 579 = 3474 7 × 579 = 4053 8 × 579 = 4632 9 × 579 = 5211

Step 5 With a target of 4329, the closest we can get is 4053 by multiplying 579 by 7. Write the 4053 below the 4329 as shown.	9 1 7  rem 276 579 5 3 1 2 1 9 5 2 1 1 1 0 1 1 5 7 9 4 3 2 9 4 0 5 3
579 × table 1 × 579 = 579 2 × 579 = 1158 3 × 579 = 1737 4 × 579 = 2316 5 × 579 = 2895 6 × 579 = 3474 7 × 579 = 4053 8 × 579 = 4632 9 × 579 = 5211

Step 6 Finally, subtract 4053 from 4329 giving 276. Since there are no other digits to bring down, 276 is therefore also the remainder for the whole sum. So 531219 ÷ 579 = 917 rem 276	9 1 7  rem 276 579 5 3 1 2 1 9 5 2 1 1 1 0 1 1 5 7 9 4 3 2 9 4 0 5 3 2 7 6
579 × table 1 × 579 = 579 2 × 579 = 1158 3 × 579 = 1737 4 × 579 = 2316 5 × 579 = 2895 6 × 579 = 3474 7 × 579 = 4053 8 × 579 = 4632 9 × 579 = 5211

[Read More...]

How to do long division with remainders?

 
Master Long Division Practice Workbook: Improve Your Math Fluency Series (Volume 8)

Basic Math and Pre-Algebra Workbook For Dummies 

Division, Ages 7-12 (Workbook w/Music CD) 

 

Solution for 768978 ÷ 358 - with remainder

Step 1 Long division works from left to right. Since 358 will not go into 7, a grey 0 has been placed over the 7 and we combine the first two digits to make 76. In this case, 76 is still too small. A further 0 is added above 6 and a third digit is added to make 768. Note the other digits in the original number have been turned grey to emphasise this. The closest we can get to 768 without exceeding it is 716 which is 2 × 358. These values have been added to the division, highlighted in red.

0 0 2  rem 352 358 7 6 8 9 7 8 7 1 6

358 × table 1 × 358 = 358 2 × 358 = 716 3 × 358 = 1074 4 × 358 = 1432 5 × 358 = 1790 6 × 358 = 2148 7 × 358 = 2506 8 × 358 = 2864 9 × 358 = 3222

Step 2 Next, work out the remainder by subtracting 716 from 768. This gives us 52. Bring down the 9 to make a new target of 529.	2  rem 352 358 7 6 8 9 7 8 7 1 6 5 2 9
358 × table 1 × 358 = 358 2 × 358 = 716 3 × 358 = 1074 4 × 358 = 1432 5 × 358 = 1790 6 × 358 = 2148 7 × 358 = 2506 8 × 358 = 2864 9 × 358 = 3222

Step 3 With a target of 529, the closest we can get is 358 by multiplying 358 by 1. Write the 358 below the 529 as shown.	2 1  rem 352 358 7 6 8 9 7 8 7 1 6 5 2 9 3 5 8
358 × table 1 × 358 = 358 2 × 358 = 716 3 × 358 = 1074 4 × 358 = 1432 5 × 358 = 1790 6 × 358 = 2148 7 × 358 = 2506 8 × 358 = 2864 9 × 358 = 3222

Step 4 Next, work out the remainder by subtracting 358 from 529. This gives us 171. Bring down the 7 to make a new target of 1717.	2 1  rem 352 358 7 6 8 9 7 8 7 1 6 5 2 9 3 5 8 1 7 1 7
358 × table 1 × 358 = 358 2 × 358 = 716 3 × 358 = 1074 4 × 358 = 1432 5 × 358 = 1790 6 × 358 = 2148 7 × 358 = 2506 8 × 358 = 2864 9 × 358 = 3222

Step 5 With a target of 1717, the closest we can get is 1432 by multiplying 358 by 4. Write the 1432 below the 1717 as shown.	2 1 4  rem 352 358 7 6 8 9 7 8 7 1 6 5 2 9 3 5 8 1 7 1 7 1 4 3 2
358 × table 1 × 358 = 358 2 × 358 = 716 3 × 358 = 1074 4 × 358 = 1432 5 × 358 = 1790 6 × 358 = 2148 7 × 358 = 2506 8 × 358 = 2864 9 × 358 = 3222

Step 6 Next, work out the remainder by subtracting 1432 from 1717. This gives us 285. Bring down the 8 to make a new target of 2858.	2 1 4  rem 352 358 7 6 8 9 7 8 7 1 6 5 2 9 3 5 8 1 7 1 7 1 4 3 2 2 8 5 8
358 × table 1 × 358 = 358 2 × 358 = 716 3 × 358 = 1074 4 × 358 = 1432 5 × 358 = 1790 6 × 358 = 2148 7 × 358 = 2506 8 × 358 = 2864 9 × 358 = 3222

Step 7 With a target of 2858, the closest we can get is 2506 by multiplying 358 by 7. Write the 2506 below the 2858 as shown.	2 1 4 7  rem 352 358 7 6 8 9 7 8 7 1 6 5 2 9 3 5 8 1 7 1 7 1 4 3 2 2 8 5 8 2 5 0 6
358 × table 1 × 358 = 358 2 × 358 = 716 3 × 358 = 1074 4 × 358 = 1432 5 × 358 = 1790 6 × 358 = 2148 7 × 358 = 2506 8 × 358 = 2864 9 × 358 = 3222

Step 8 Finally, subtract 2506 from 2858 giving 352. Since there are no other digits to bring down, 352 is therefore also the remainder for the whole sum. So 768978 ÷ 358 = 2147 rem 352	2 1 4 7  rem 352 358 7 6 8 9 7 8 7 1 6 5 2 9 3 5 8 1 7 1 7 1 4 3 2 2 8 5 8 2 5 0 6 3 5 2
358 × table 1 × 358 = 358 2 × 358 = 716 3 × 358 = 1074 4 × 358 = 1432 5 × 358 = 1790 6 × 358 = 2148 7 × 358 = 2506 8 × 358 = 2864 9 × 358 = 3222

[Read More...]